考虑这样一个具有一般性的问题:给定一个数组A,和两个元素间的简单关系P,找出A中每一个元素\(A[i]\),在其后面的第一个元素\(A[j](j > i)\),使得\(A[i]\)和\(A[j]\)满足关系P。
解决这类问题的一个高效方法就是单调栈。单调栈原理的关键就在于关系P是只关于两个元素的,从而每个元素在找第一个满足关系P的元素时,有大量的检验是重复的,而单调栈可以避免这些重复。
关于单调栈的原理,可以看这篇文章:数据结构的应用篇【1】:单调栈
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指在第 i 天之后,才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
LeetCode 739
这道题是使用单调栈的经典问题,本质上就是让你求数组中每一个元素在其后面的第一个更大的元素,只是这里要的是它们的索引距离。如果使用传统方法,对每一个元素都往后遍历,那么时间复杂度就是\(O(n^{2})\) ,而使用单调栈的时间复杂度是\(O(n)\) 。
具体来说,遍历一次数组,将未解决的元素依次入栈,若是当前元素大于栈顶元素,那么说明栈顶元素已经解决(当前元素即是它在其后的第一个更大的元素),此时栈顶元素出栈。然后不断检查新的栈顶元素,直到当前元素不大于栈顶元素,此时栈顶元素还未解决(因为还没遇到比它大的元素),那么将当前元素入栈,并继续遍历。每次元素出栈时,记录它们的索引距离。
栈中储存的是元素的索引,而不是元素的值,因为通过索引我们一般都能很简单的得到元素的值,但是反过来就不一定了。而且记录索引值可以帮助我们计算距离。
注意到,单调栈解决元素的顺序和数组中元素的顺序不一样,而是和元素的大小有关,这是因为栈中元素一直保持单调,从而每次遇到较大元素时,可以一次性解决多个元素。
对于第一个元素而言,因为此时栈为空,所以无从比较,要特殊处理。但我们可以利用哨兵避免这个情况,只需在原数组前加入一个非常大的元素(此题中温度最高是100,所以比100大的值都可以,代码中选取了200),使得第一个元素满足入栈条件即可。
一次遍历结束后,栈一定是非空的,至少最后一个元素还在栈中,因此需要在遍历结束后再将栈中剩余元素依次解决。
C#代码如下:
public class Solution {
public int[] DailyTemperatures(int[] temperatures) {
Stack<int> stack = new Stack<int>();
List<int> list = new List<int>(temperatures);
int[] ret = new int[temperatures.Length];
list.Insert(0, 200);
stack.Push(0);
for(int i = 1; i < list.Count; i++)
{
while(list[i] > list[stack.Peek()])
{
int pop = stack.Pop();
ret[pop - 1] = i - pop;
}
stack.Push(i);
}
while(stack.Count != 1)
{
ret[stack.Pop() - 1] = 0;
}
return ret;
}
}
在具体问题中,所要求的东西不一样,但是本质都是定位,定位之后再想办法求就行。为了记录的方便,也可以根据情况改变栈中储存的信息。例如:
LeetCode 901 股票的价格跨度
这道题通过类调用的形式检查答案,这个时候就没有现成的数组和索引值了。但可以通过一个计数变量记录当前价格的索引,然后使用元组作为栈的数据结构,在元组中同时储存价格和索引,可以实现同样的效果。
public class StockSpanner {
const int max = 100001;
int N = 1;
Stack<(int price, int index)> stack = new Stack<(int price, int index)>();
public StockSpanner() {
stack.Push((max, N++));
}
public int Next(int price) {
while(price >= stack.Peek().price)
{
stack.Pop();
}
int ret = N - stack.Peek().index;
stack.Push((price, N++));
return ret;
}
}
接下来是两道稍有难度的题目:
LeetCode 84 柱状图中的最大矩形
这道题对单调栈的考察并不是直接。题目所要求的最大矩形,可以通过枚举高度求得,具体来说,对每一个柱子,按它自身高度往两边进行扩散,直到遇到比它矮的柱子为止,那么这个柱子所扩散的最大面积便确定了,就是左右遇到的两个矮柱子之间的距离(不包括矮柱子)乘以这个柱子的高度。换句话说,我们需要求出每一个柱子,在其前面的第一个(离它最近)比它矮的柱子,和在其后面的第一个比它矮的柱子。这启发我们使用单调栈算法。
看起来,这道题需要我们求出两个方向的满足关系的最近元素,但仔细想一下,实际上我们只需要求一个方向的就行了。以求柱子A往右第一个比它矮的柱子为例,当我们向右遇到第一个比A矮的柱子时,说明A最大扩散矩形的右边界已经确定了,左边界有没有确定呢?答案是有的,左边界即是栈中A柱子下面的柱子,即A出栈后的新的栈顶元素所代表的柱子。这是因为单调栈总是保持递增顺序,在A左边且比A高的柱子早在之前便出栈了,所以A出栈后的新的栈顶元素,一定是往左离A最近的比它矮的柱子。这是单调栈的一个重要性质。
也就是说,向右遇到比栈顶元素\(pop\)代表的柱子还矮的柱子时,栈顶元素代表的柱子的最大扩散矩形已经确定了,右边界即是当前遍历到的元素(矮柱子)\(i\),左边界即下一个新的栈顶元素\(peek\)。假设栈中储存的是索引,那么宽度即是\(i - peek - 1\) ,最大扩散矩形的面积即\((i - peek - 1) * heights[pop]\) 。
对于第一根柱子,我们可以采用哨兵机制避免特殊情况。在这里,让哨兵严格最小即可。对于栈中剩余的柱子,我们也可以在高度数组末尾增加哨兵来解决,由于最后往右没有矮柱子了,只需让尾部的哨兵也严格最小即可。这样栈中最后剩余的就是这两个哨兵了。时间复杂度是\(O(n)\) 。
C#代码如下:
public class Solution {
public int LargestRectangleArea(int[] heights) {
List<int> h = new List<int>(heights);
Stack<int> stack = new Stack<int>();
int peek, pop, now, max = 0;
//哨兵
h.Insert(0, 0);
h.Add(0);
stack.Push(0);
//从1开始
for(int i = 1; i < h.Count; i++)
{
while(h[i] < h[stack.Peek()])
{
pop = stack.Pop();
peek = stack.Peek();
now = (i - peek - 1) * h[pop];
if(now > max)
{
max = now;
}
}
stack.Push(i);
}
return max;
}
}
第二道题是 LeetCode 85 最大矩形
这道题要求的是一个二进制矩阵中只含1且最大的子矩阵的面积。与上一题相比,这道题是二维的,所以暴力处理起来更困难。不过可以利用上一题的结论来解决。
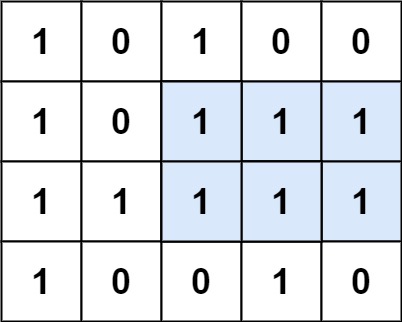
考虑选定矩阵的某一列元素,以上图最后一列为例,可以看出,以这一列的连续元素(部分或全部)为一条边往左扩散的最大只含1矩形,是和这一列各元素往左连续1的数量(包括本身)有关的。准确地说,最后一列各元素的往左连续1的数量是\({0, 3, 4, 0}\) ,这刚好构造了一个竖向的柱状图(下图绿色部分),连续1数量即是柱的高度,而以这一列为一条边往左扩散的最大的只含1矩形,就是这个柱状图所能描绘的最大矩形(下图红色边框部分)。
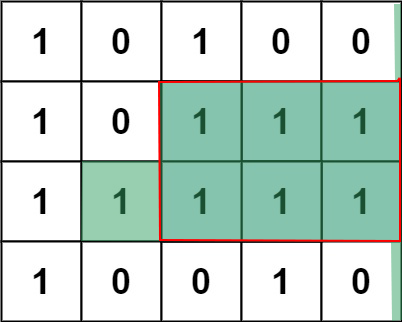
所以问题就很简单了,对每一列,记录往左连续1数量,然后按上题的方法依次计算每一列满足的只含1的矩形的面积,并取最大值即可。对 \(m*n\) 矩阵,时间复杂度为\(O(mn)\) 。
C#代码如下:
public class Solution {
public int LargestRectangleArea(int[] heights) {
List<int> h = new List<int>(heights);
Stack<int> stack = new Stack<int>();
int peek, pop, now, max = 0;
//哨兵
h.Insert(0, 0);
h.Add(0);
stack.Push(0);
//从1开始
for(int i = 1; i < h.Count; i++)
{
while(h[i] < h[stack.Peek()])
{
pop = stack.Pop();
peek = stack.Peek();
now = (i - peek - 1) * h[pop];
if(now > max)
{
max = now;
}
}
stack.Push(i);
}
return max;
}
public int MaximalRectangle(char[][] matrix) {
int rows = matrix.Length;
int cols = matrix[0].Length;
int[][] one = new int[cols + 1][];
for(int i = 0; i < cols + 1; i++)
{
one[i] = new int[rows + 1];
}
for(int i = 0; i < rows; i++)
{
for(int j = 0; j < cols; j++)
{
if(matrix[i][j] == '0')
{
one[j + 1][i + 1] = 0;
}
else
{
one[j + 1][i + 1] = one[j][i + 1] +
(matrix[i][j] == '1' ? 1 : 0);
}
}
}
int max = 0;
for(int i = 1; i <= cols; i++)
{
max = Math.Max(max, LargestRectangleArea(one[i]));
}
return max;
}
}